Gzalo

Final 10 de agosto de 2015

Se define una estructura tnodo con un cierto campo valor (de cualquier tipo) y *sig, puntero a tnodo. Hay dos vectores de punteros,

tnodo *VE[100], tnodo *VCOL[100]

El primero es un vector de punteros a listas (de distintas longitudes -obviamente pueden haber 2 o más con la misma longitud-), con NULL en la última posición.

Hay que hace un procedimiento void elim_cols(tnodo *VE, tnodo *VCOL) que realice lo siguiente: Que desenganche (removiéndolas de la lista correspondiente) las columnas impares de cada lista (formadas por los nodos del vector de listas que estén a una misma profundidad), y las enganche entre sí, guardando el primer nodo de cada columna en un puntero de una posición del vector de VCOL. Es decir que el *sig de cada nodo de cada columna impar, debe apuntar al nodo de abajo de la columna, y el nodo anterior (el de la columna par) debe apuntar al nodo siguiente al de la columna impar. Los nodos finales de cada lista tendrán sig=NULL.

Realizar una función que ordene un vector usando solamente recursividad, aplicando el método de Selección. La función puede recibir por parámetro solamente al vector y a su cantidad de elementos. Todas las sub-funciones que se usen deben usar recursividad (pueden recibir más variables por parámetro). No se puede usar nada iterativo.

Final 4 de julio de 2013

Hay dos listas de personas, una de padres y una de hijos.

struct persona{
	char nombre[20];
	char antecesor[20];
	persona *sig;
};

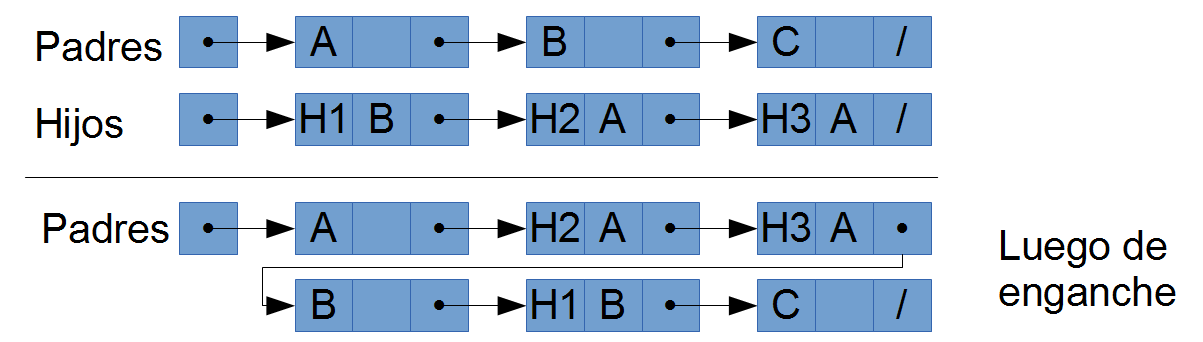
Hay que escribir un procedimiento void enganchar(persona *padres, persona **hijos); que cambiase la lista de padres de tal manera que la lista quedara de la siguiente forma: A → 1er hijo de A → 2do hijo de A → B → 1er hijo de B → C → NULL

Es decir, que estén los padres ordenados según el mismo orden que la lista original, pero que entre ellos estén todos los hijos correctos.

Dadas las siguientes estructuras:

struct alumno{
	char nombre[20];
	int nota;
	alumno *sig2;
	alumno *sig;
};
struct materia{
	char nombre[20];
	alumno *prim;
};

Hay un vector de materias. La última materia tiene un NULL en el campo prim.

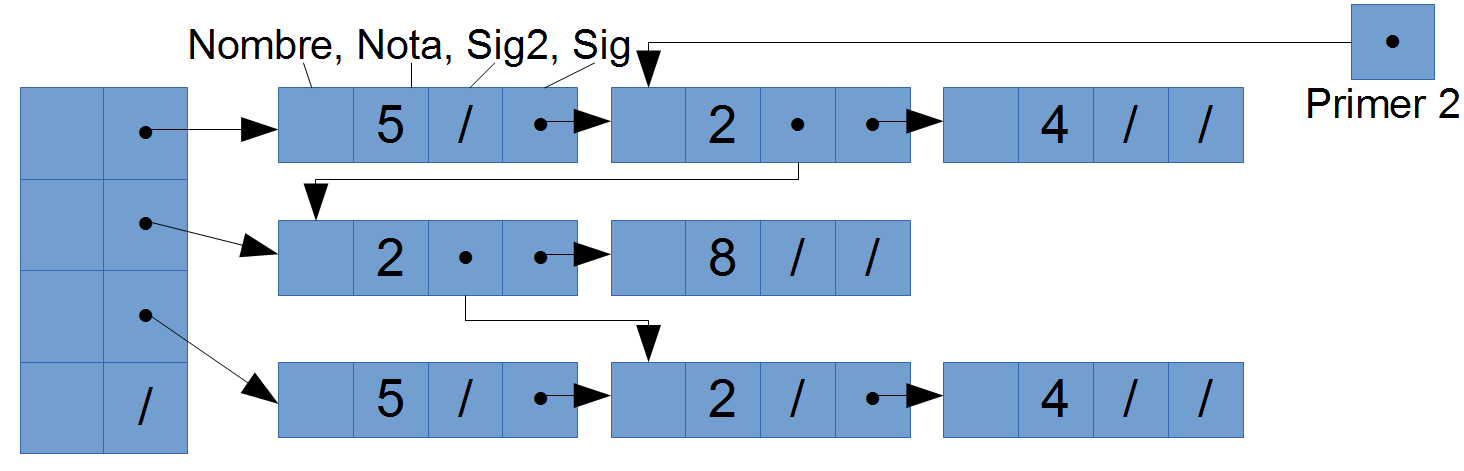
Escribir un procedimiento void enganchar(materia *materias, alumno **primer2); que enganche a los alumnos que tienen nota 2, poniendo el primero de ellos en la variable primer2, de tal forma que recorriendo por sig2 pases por todos ellos.

Final 8 de julio de 2013

Dada una matriz cuadrada imprimir las celdas recorriendo en forma de reloj de arena:

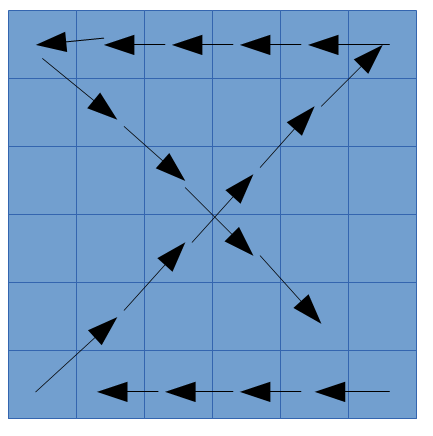
Variantes: matriz de ancho par/impar, misma forma de recorrer pero rotada 90º.

Dado un vector de listas, ordenarlas según longitud (cantidad de elementos en la lista):

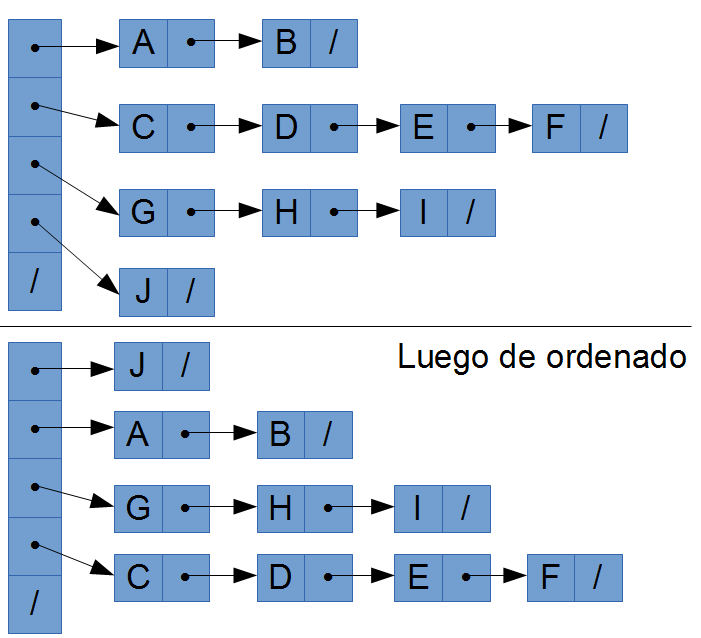
Variantes: sin usar/usando un vector auxiliar para guardar la longitud de cada lista.

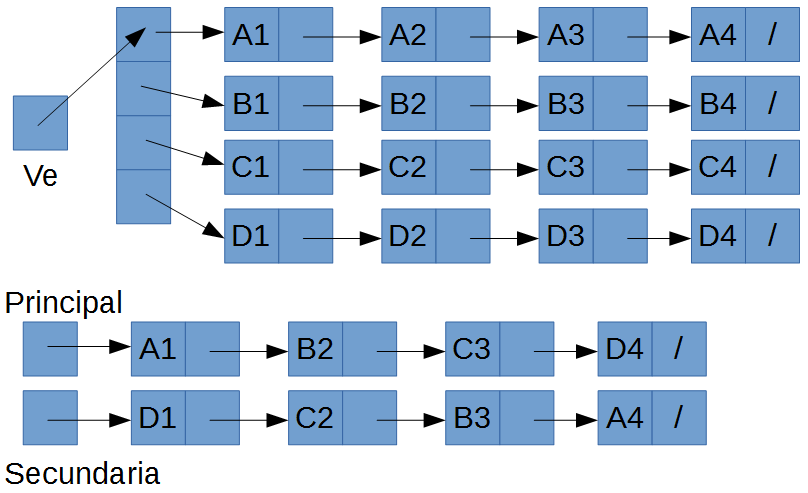
Dado un vector de listas como se ve en la figura (cuadrado), se pide enganchar la Diagonal principal y secundaria, descartando esos nodos del vector original y además si hay un nodo compartido (si la longitud es impar), no agregarlo a la diagonal secundaria.

Extras de otros finales

• Ordenamiento de vector de enteros por selección/burbujeo de manera recursiva.
• Un archivo tiene muchos enteros, cada uno en una línea. Obtener los 100 valores máximos de ellos, leyendo el archivo 1 sola vez y sin guardarlo todo en memoria. Variantes: cadenas de texto en lugar de enteros
• Recorrer una matriz (tanto cuadrada como rectangular) en forma de caracol, tanto de forma iterativa como recursiva.
• Enganchar un vector de listas de tal manera que al recorrerla haga forma de Z o X: 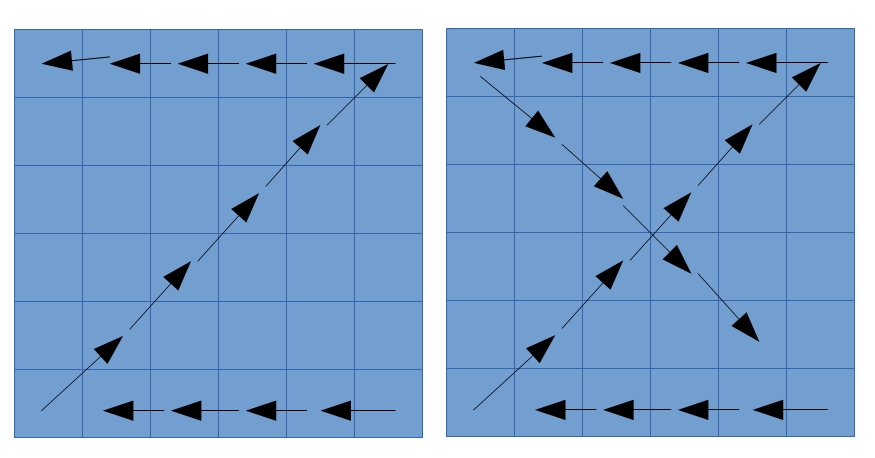(cada cuadrado representa un nodo, están enganchados horizontalmente)
• Enganchar un vector de listas de manera de recorrerlo por columnas, es decir: primer nodo de primera lista → primer nodo de segunda lista → … → segundo nodo de primera lista → …
• Dada una matriz de enteros, escribir una función que diga en qué celda (qué fila y columna) es máxima la suma de los valores de las celdas vecinas. Variantes: conectividad4/8 (incluyendo y no incluyendo vecinos en diagonal), warpeado (la matriz es un toroide/dona, los vecinos se repiten horizontal y verticalmente)

Ejercicios resueltos enviados por Fernando Filippetti (pueden contener errores)

Última actualización: Febrero de 2017